Introduction to Critical Value in Statistics: Explained with Types & Examples

The curve is split into two sections by the critical value; one of these regions is the acceptance region, while the other is the rejection zone. The null hypothesis is rejected and the alternative hypothesis is accepted if the test statistics value is inside the rejection (critical) zone.

The crucial value indicates whether the null hypothesis is accepted or rejected during hypothesis testing. In contrast to the two-tailed test, which has two critical values, the one-tailed test only has one critical value. Various hypothesis tests are calculated using the crucial value.

How to Calculate Critical Value?

Let’s learn how to find critical value for a one-tailed and two-tailed test. By using confidence level, we can find critical value easily. Consider the confidence level that is 90%. Follow the following steps to evaluate the critical value,

• Subtract the confidence level from 100 percent to determine the alpha (level of significance). Alpha = 100% – 90% = 10% as a result. 
• Convert the alpha value to decimal, so 10% is equivalent to 0.1. 
• We apply the aforementioned strategy to the one-tail test. However, we must divide the degree of alpha by two if we want two-tail tests.

Types of Critical Value

The critical value is of four types:

1. T – Critical value
2. Z – Critical value
3. F – Critical value
4. Chi-square critical value

Here, we will discuss its types in detail.

• T-Critical value 

It is used when,

• n < 30, where n is the sample size
• Population standard deviation is not given 

How to Calculate the T – critical value?

• First of all, find the level of significance 
• To find the degree of freedom (df), subtract 1 from sample size n. 
• Now look at the t- distribution table 
• Observe the degree of freedom (df) at the left side column and alpha at the top row of the t-table. Then take the corresponding value of this row and column. The resulting value will be t-critical value.

• Z – Critical value

When we use z-tests 

•  n ≥ 30
• If the Population standard deviation is given as input

How to find the Z – critical value?

• Evaluate the level of significance (alpha α). 
• For the one-tailed test, alpha is subtracted from 0.5, and for the two-tailed test, alpha subtracts from 1.
• Now, look Z table to give the z-critical value.
• After the calculation of the left-tailed test, we will write a negative sign at the end of the calculations.

• F – Critical value

 To compare the variance of two samples, F-critical value is used. In the F-critical value, two sample sizes are given. The f-critical value test is also known as ANOVA.

How to find the F – critical value?

• First, calculate the level of significance (alpha α). 
• To get 1st degree of freedom (df), 1 subtract from 1st sample size (n1) and say x = n1 – 1 
• To get 2nd degree of freedom (df), 1 subtract from 2nd sample size (n2) and say y = n2 – 1 
• Now look at the f- distribution table and take the corresponding value of the x column and y row to get the f- critical value.

• Chi-Square Critical value

 In the chi-square value, we compare two variables to determine the relationship between them.

How to calculate the Chi-Square critical value?

• • Determine the level of significance (alpha α). 

• To get the degree of freedom (df), 1 subtract from the sample size i.e. df = n – 1

• To get Chi-square critical value, look at the chi-Square distribution table and take the intersection of the alpha column and degree of freedom row.

Examples

Example 1:

Find a one-tail test when the level of confidence is 99% and the sample size is 5.

Solution:

Here, n = 5, and n < 30, so we will use a t-test.

Step 1: To find alpha, subtract the level of confidence from 100% i.e.

Alpha = 100% – 99% = 1%

Step 2: Covert alpha into decimal 

Alpha = α = 1 / 100 = 0.01

Step 3: To get the degree of freedom (df), subtract 1 from the sample size.

df = 5 – 1 = 4

Step 4: Then look at t- distribution table

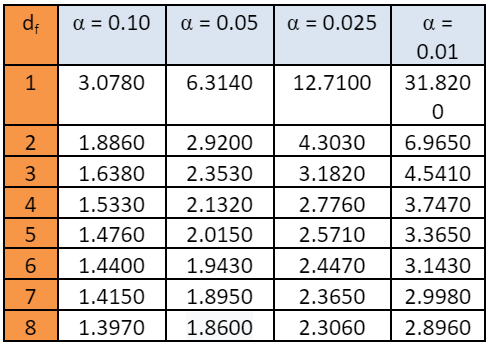
Step 5: In the t-distribution table, locate the degree of freedom (4) in the left side column and alpha (0.01) in the top row. Take the value at the point where this row and this column cross; this is our T-critical value.

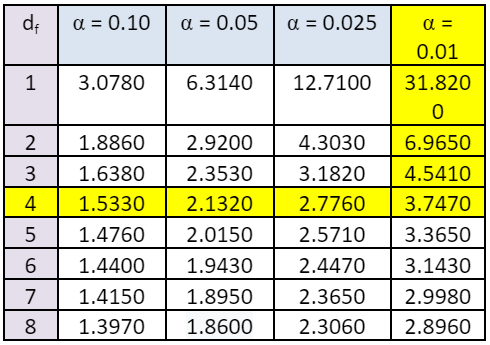
The degree of freedom and alpha intersect at 3.7470, so it is our t-critical value.

Applications of Critical Value:

In statistical hypothesis testing and confidence interval estimation, critical values are frequently utilized. The following are a few significant uses of critical values:

• Hypothesis Testing Process: Critical values are used in hypothesis testing to decide whether to reject or not reject a null hypothesis. To get a conclusion, the critical value and test statistic are compared. The null hypothesis is rejected in favor of the alternative hypothesis if the test statistic is greater than or less than the crucial value.
• Confidence Intervals: Confidence intervals are created using critical values. For an unknown parameter, a confidence interval offers a range of likely values, and the crucial value is used to calculate the margin of error or the breadth of the interval. The required degree of confidence (for example, a 95% confidence interval) is often the basis for the crucial value.
• Significance Levels: Significant levels and critical values determine the likelihood that the null hypothesis will be rejected when it is truly true. The significance values of 0.05 (5%) and 0.01 (1%) are frequently employed. The cutoff point for rejecting the null hypothesis is determined using the critical value corresponding to the selected significance level.

Summary

In the above article, we have studied the concept of critical value in statistics along with its types. This concept is of much importance in the field of statistical hypotheses and others. After understanding its concept, we can easily solve as many problems as we have.